Linear motion
Observe the things around you. Some of the objects you see are stationery.For example, buildings, statues and rocks. Some of the objects are moving. A fanrotating, vehicles moving on the road and birds flying are some examples of moving objects. If you observe the motion of the moving objects more closely, you will be
able to observe the nature of their motion more clearly (fig 3.1.1). The rotating fan shows a rotational motion. Motion of planets around the sun is referred to as revolution.The motion of a pendulum bob is an oscillation. A runner of 100 metres running along a straight track undergoes a linear motion. In this chapter let us
understand some concepts related to the linear motion.
Distance and Displacement
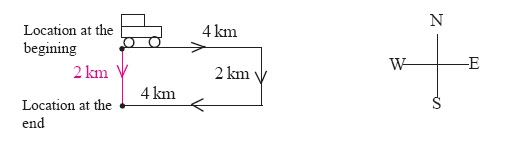
Assume that you are walking to school. The length of the path that you moved on your way is known as ‘distance’. Therefore, the length moved by a moving object is the distance travelled by it.Consider the linear motion of a motor vehicle shown in fig 3.1.2. The vehiclemoves 4 km to the East, 2 km to the South and then 4 km to the west.
The magnitude of the distance moved by the motor vehicle = (4+ 2 + 4 ) km
= 10 km
But, when considering the direction of motion of the vehicle, at the beginning it moved to the East, then to the South and finally to the West. Hence, it does not show the motion in a definite direction. Therefore, the quantity of distance has a magnitude but no definite direction.Such quantities which have a magnitude but no direction are called scalar quantities. Accordingly, distance is a scalar quantity.Now let us consider the quantity called displacement.Refer to the fig 3.1.2 again. Although the vehicle moved 10 km from the starting
point to the final point, the change in the position of the object is only 2 km towards the south direction.
Quantities with both a direction and a magnitude are known as vector quantities.Accordingly displacement is a vector quantity.
Solved problem 1
A student walks 2 km along a linear path to the West then turns around and walks 2 km along the same path to the East. Find the distance and the displacement of the student.
Distance travelled = 2 km + 2 km = 4 km
Displacement = 0 km
Solved problem 2
A motor car travelled 10 km along a straight road to the East, turned around and travelled 7 km to the West.
Find the distance and the displacement of the car.
Distance travelled = 10 km + 7 km = 17 km
Displacement = 3 km to the East
Speed
The rate of the change of distance is known as the speed. If the distance travelled per unit time is low the speed of the object is low. If the distance travelled per unit time is high, the speed of the object is high. Recall your experience of travelling in a bus. If you observe the speedometer you will realize that the speedometer reading is changing from moment to moment. The reading of the speedometer of the bus at a given time
shows its speed. If the speedometer reading is constant for a given period of time, we say that the bus has travelled at a constant speed.If an object moves equal distance in equal time intervals, it is said that the object
moves at a constant speed. The speed of an object could be given by the following equation
Speed = Distance travelled
Time taken
The speed of an object is the distance travelled in a unit time .The SI unit of speed is metres per second. (m s-1).
Average Speed
Vehicles do not always travel at same speed. Sometimes they travel faster sometimes slower. Therefore we have to refer an average speed rather than the speed.The average speed of an object could be calculated by using the following equation
Average speed = Total distance moved
Total time taken
SI unit for average speed is also metres per second.e.g. The average speed of a van travelling 60 m in 6 s could be calculated as follows,
Therefore the average speed of the van is 10 m s-1 If the distance travelled are long, we indicate the speed in kilometres per hour(km h-1) Speed has a magnitude but no direction. Hence, it is a scalar quantity.


No comments:
Post a Comment